Water Tank Capacity Calculator

   

---

---

What is a Water Tank Capacity Calculator?

A water tank capacity calculator is a simple free online tool that helps you figure out how much liquid a tank can hold. Instead of guessing, you have to enter the tank’s dimensions: length, width, height, diameter or depth depending on the shape and the calculator does the math instantly and give you results.

People use it for all sorts of things. Maybe you’re sizing a storage tank for rainwater harvesting Or you are a contractor who needs to check if a cylindrical tank will fit a client’s daily water demand. Farmers often rely on it for livestock water tanks, while some homeowners just want to know if their tank is big enough for daily household use.

Without a calculator, you’d be stuck scribbling formulas on paper or searching through geometry textbooks But with the help of this tool, you just have to enter the values and when you tap on calculate you will get the results in liters, gallons and cubic feet.

Types of Water Storage Tanks

Not all tanks are shaped the same way and that’s where a water tank capacity calculator really shines. Tanks can be simple boxes, tall vertical cylinders or even complex shapes like capsules and cone bottom designs. Each type requires its own formula to correctly calculate how much liquid it can hold

Here’s a simple guide to the most common water tank shapes and how people use them:

1. Rectangle (Rectangular Prism or Box): A basic non curved shape with flat surfaces.
   • Commonly used for small household water tanks, aquariums and storage containers because they’re easy to build and install.
2. Vertical Cylinder: A cylindrical tank standing upright.
   • Widely used for water towers, rainwater harvesting and industrial storage, since they take up less ground space.
3. Horizontal Cylinder: A cylindrical tank lying on its side.
   • Often used in transportation (trucks, trailers) and for fuel or liquid storage where stability is needed.
4. Vertical Capsule: A vertical version of the capsule tank.
   • Useful for space saving vertical storage in factories or plants where durability is important.
5. Horizontal Capsule: A cylinder with rounded ends, lying on its side.
   • Popular in liquid transport and chemical industries since the rounded ends reduce stress points.
6. Vertical Oval: An oval-shaped tank standing upright.
   • Suitable for basements, factories or tight indoor spaces where width is limited but height is available.
7. Horizontal Oval: An oval-shaped tank lying sideways.
   • Handy for limited height spaces like under decks or in crawl areas where a round cylinder won’t fit.
8. Horizontal 2:1 Elliptical: A special elliptical shape with a 2:1 aspect ratio, often seen in tank heads.
   • Common in pressure vessels and industrial tanks offering strength while saving material.
9. Horizontal Ellipse: An elliptical cross-section tank, horizontally oriented.
   • Used in transport and process industries as the flatter design lowers the center of gravity.
10. Vertical Oval Stadium: A vertically standing tank with a “stadium” cross-section (a rectangle with semicircle ends).
    • Useful in factories or buildings where a tall, slim profile is needed but with more capacity than a plain oval.
11. Horizontal Oval Stadium: A horizontally oriented tank with a “stadium” cross-section.
    • Often chosen for transport and storage in low clearance areas since the flat sides allow stacking or fitting in tighter spaces.
12. Horizontal Dish Ends: Cylindrical tank with dished (curved) end caps.
    • Found in high-pressure storage, chemical plants and breweries, as the dish ends handle pressure better.
13. Spherical: A perfectly round tank.
    • Typically used for large scale gas storage (like LPG or LNG) due to uniform stress distribution.
14. Cone Bottom: A vertical cylindrical tank with a conical base.
    • Common in food processing, wastewater treatment and brewing, since the cone allows complete drainage.

Water Tank Capacity Calculation Formula

When designing or using a water tank, knowing its storage capacity is important for proper planning in homes, industries or in agriculture. The capacity depends on the tank’s shape and can be calculated using standard formulas of geometry. The following sections explain the formulas for different tank types with solved examples and results converted into liters for easy understanding.

Here’s a quick breakdown of the formulas used in the calculator for different shapes:

1: Rectangular Prism

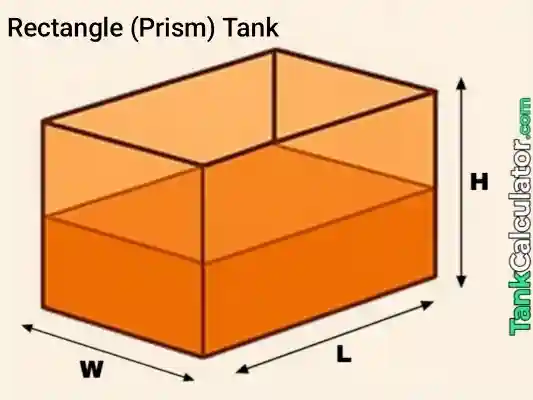
Formula: \( V = L \times W \times H \)

Example inputs: \( L = 0.8 \, \text{m}, W = 0.6 \, \text{m}, H = 0.5 \, \text{m} \)

Calculation:

1. \( 0.8 \times 0.6 = 0.48 \)
2. \( 0.48 \times 0.5 = 0.24 \, \text{m}^3 \)

Convert to liters: \( 0.24 \times 1000 = 240.000 \, \text{L} \)

2: Vertical Cylinder

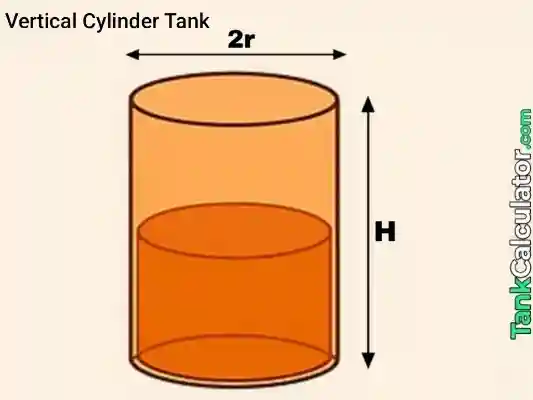
Formula: \( V = \pi \left(\frac{D}{2}\right)^2 H \)

Example inputs: \( D = 0.6 \, \text{m}, H = 1.0 \, \text{m} \)

Calculation:

1. \( r = D/2 = 0.6/2 = 0.3 \, \text{m} \)
2. \( r^2 = 0.3^2 = 0.09 \)
3. \( \pi r^2 H = \pi \times 0.09 \times 1.0\)
   • \(= 0.2827433388 \, \text{m}^3 \)

Convert to liters: \( 0.2827433388 \times 1000 = 282.743 \, \text{L} \)

3: Horizontal Cylinder

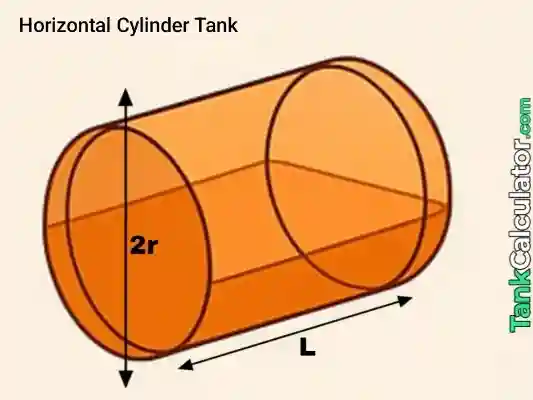
Formula: \( V = \pi \left(\frac{D}{2}\right)^2 L \)

Example inputs: \( D = 0.5 \, \text{m}, L = 1.0 \, \text{m} \)

Calculation:

1. \( r = 0.25 \, \text{m} \)
2. \( r^2 = 0.0625 \)
3. \( \pi \times 0.0625 \times 1.0\)
   • \( = 0.1963495408 \, \text{m}^3 \)

Convert to liters: \( 0.1963495408 \times 1000 = 196.350 \, \text{L} \)

4: Vertical Capsule

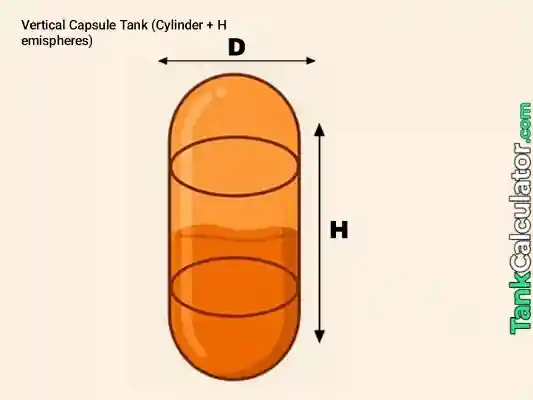
Formula: \( V = \pi r^2 H_c + \frac{4}{3} \pi r^3 \) where \( r = D/2 \)

Example inputs:  \( D = 0.5 \, \text{m}, H_c = 0.6 \, \text{m} \)

Calculation:

1. \( r = 0.25 \, \text{m} \)
2. Cylinder: \( \pi r^2 H_c = \pi \times 0.0625 \times 0.6\)
   • \( = 0.1178096885 \, \text{m}^3 \)
3. Hemispheres combined = sphere: \( \frac{4}{3} \pi r^3 = \frac{4}{3} \pi \times 0.015625 \)
   • \(= 0.0654498829 \, \text{m}^3 \)

Total: \( 0.1178096885 + 0.0654498829\)

\( = 0.1832595714 \, \text{m}^3 \)

Convert to liters: \( 0.1832595714 \times 1000 = 183.260 \, \text{L} \)

5: Horizontal Capsule

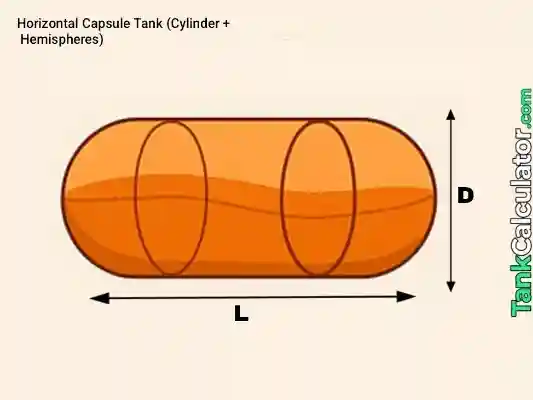
Formula: \( V = \pi r^2 L_c + \frac{4}{3} \pi r^3 \)

Example inputs: \( D = 0.45 \, \text{m}, L_c = 0.8 \, \text{m} \)

Calculation:

1. \( r = 0.225 \, \text{m} \)
2. \( r^2 = 0.050625 \)
3. Cylinder: \( \pi \times 0.050625 \times 0.8 \)
   • \(= 0.1274971969 \, \text{m}^3 \)
4. Hemispheres combined: \( \frac{4}{3} \pi r^3 = 0.0474502440 \, \text{m}^3 \)

Total: \( 0.1274971969 + 0.0474502440\)

\( = 0.1749474409 \, \text{m}^3 \)

Convert to liters: \( 0.1749474409 \times 1000 = 174.947 \, \text{L} \)

6: Vertical Oval (Elliptical cross-section)

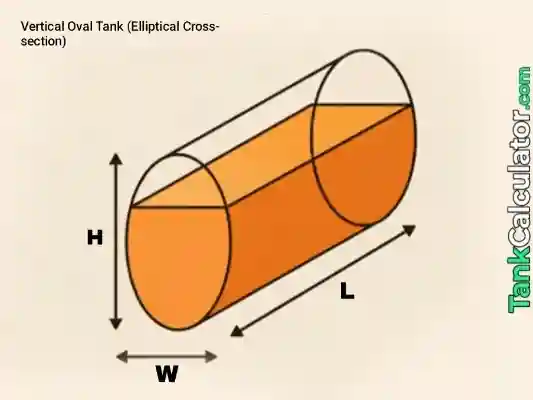
Formula: \( V = \pi \times \frac{W}{2} \times \frac{H}{2} \times L \)

Example inputs: \( W = 0.8 \, \text{m}, H = 0.5 \, \text{m}, L = 0.6 \, \text{m} \)

Calculation:

1. \( a = W/2 = 0.4, b = H/2 = 0.25 \)
2. Cross section area: \( \pi ab = \pi \times 0.4 \times 0.25 \)
   • \(= 0.3141592654 \, \text{m}^2 \)
3. Volume: \( 0.3141592654 \times 0.6\)
   • \( = 0.1884955592 \, \text{m}^3 \)

Convert to liters: \( 0.1884955592 \times 1000 = 188.496 \, \text{L} \)

7: Horizontal Oval (Elliptical cross-section)

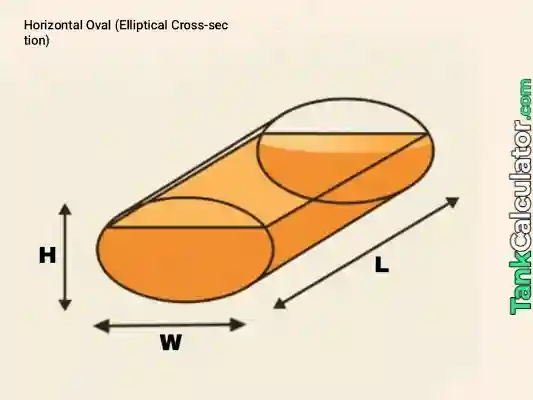
Formula: \( V = \pi \times L \times \frac{W}{2} \times \frac{H}{2} \)

Example inputs: Width (\( W \)) = 0.9 m, Height (\( H \)) = 0.4 m, Length (\( L \)) = 0.7 m

Calculation:

1. Radii: \( a = \frac{W}{2} = \frac{0.9}{2} = 0.45 \, \text{m} \), \( b = \frac{H}{2} = \frac{0.4}{2} = 0.2 \, \text{m} \)
2. Cross sectional area: \( \pi \times 0.45 \times 0.2 \)
   • \(\approx 0.2827433388 \, \text{m}^2 \)
3. Volume: \( 0.2827433388 \times 0.7 \)
   • \(\approx 0.1979203372 \, \text{m}^3 \)

Convert to liters: \( 0.1979203372 \times 1000 \approx 197.920 \, \text{liters} \)

8: Horizontal 2:1 Elliptical (major = 2 × minor)

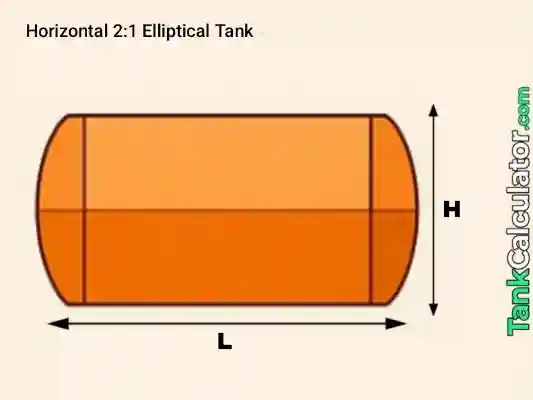
Formula: If minor = \( h \) and major = \( 2h \), \( V = \frac{\pi}{2} h^2 L \) (derived from \( \frac{\pi h}{2} \frac{L}{2} \))

Example inputs: \( h = 0.4 \, \text{m (minor)}, L = 1.2 \, \text{m} \)

Calculation:

1. \( h^2 = 0.16 \)
2. \( V = \frac{\pi}{2} \times 0.16 \times 1.2 \)
   • \(= 0.3015928947 \, \text{m}^3 \)

Convert to liters: \( 0.3015928947 \times 1000 = 301.593 \, \text{L} \)

9: Horizontal Ellipse (General Elliptical Cylinder)

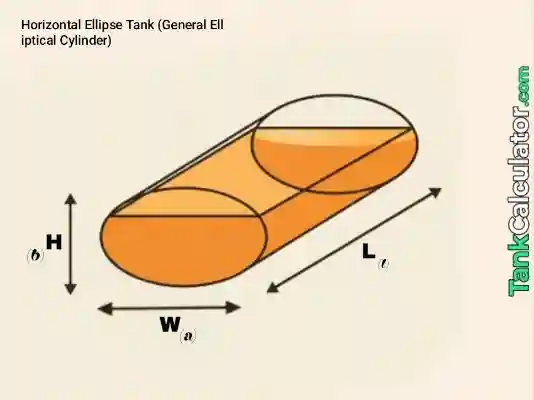
Formula: \( V = \pi \times \frac{\text{major}}{2} \times \frac{\text{minor}}{2} \times L = \pi a b L \) where \( a, b \) are semi-axes

Example inputs: major = 0.9 m, minor = 0.6 m, \( L = 0.9 \, \text{m} \)

Calculation:

1.  \( a = 0.45, b = 0.30 \)
2. Area: \( \pi \times 0.45 \times 0.30\)
   • \( = 0.4241152260 \, \text{m}^2 \)
3. Volume: \( 0.4241152260 \times 0.9\)
   • \( = 0.3817037034 \, \text{m}^3 \)

Convert to liters: \( 0.3817037034 \times 1000 = 381.704 \, \text{L} \)

10: Vertical Oval Stadium (flat tank heads)

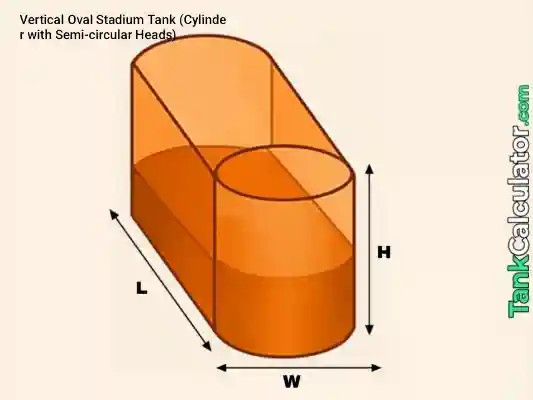
Geometry notes: Cross-section = two semicircles (radius \( r = W/2 \)) plus a central rectangle of height \( a = H – W \)

Formula: \( V = L (\pi r^2 + 2ra), r = \frac{W}{2}, a = H – W \)

Example inputs: \( W = 0.6 \, \text{m}, H = 0.9 \, \text{m}, L = 0.7 \, \text{m} \)

Calculation:

1. \( r = 0.3 \, \text{m}, a = 0.9 – 0.6 = 0.3 \, \text{m} \)
2. \( \pi r^2 = \pi \times 0.09 = 0.2827433388 \, \text{m}^2 \)
3. \( 2ra = 2 \times 0.3 \times 0.3 = 0.18 \, \text{m}^2 \)
4. Cross section area: \( 0.2827433388 + 0.18 \)
   • \(= 0.4627433388 \, \text{m}^2 \)
5. Volume: \( 0.4627433388 \times 0.7\)
   • \( = 0.3239203372 \, \text{m}^3 \)

Convert to liters: \( 0.3239203372 \times 1000 = 323.920 \, \text{L} \)

11: Horizontal Oval Stadium (flat tank cross section)

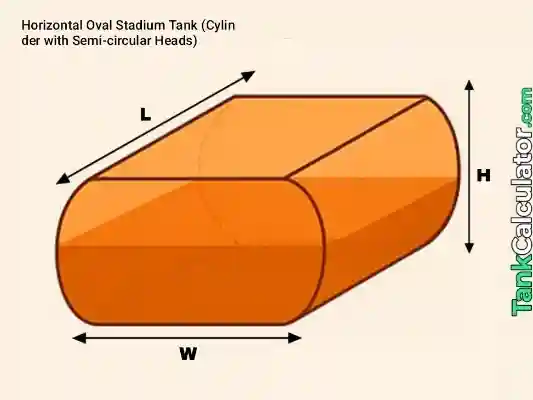
Geometry notes: Cross section = full circle (from two semicircles) of radius \( r = H/2 \) plus rectangular width \( a = W – H \)

Formula: \( V = L (\pi r^2 + a H), r = \frac{H}{2}, a = W – H \)

Example inputs:  \( W = 1.0 \, \text{m}, H = 0.5 \, \text{m}, L = 0.6 \, \text{m} \)

Calculation:

1. \( r = 0.25 \, \text{m}, a = 1.0 – 0.5 = 0.5 \, \text{m} \)
2. \( \pi r^2 = \pi \times 0.0625 = 0.1963495408 \, \text{m}^2 \)
3. \( a \times H = 0.5 \times 0.5 = 0.25 \, \text{m}^2 \)
4. Cross section area: \( 0.1963495408 + 0.25 \)
   • \( = 0.4463495408 \, \text{m}^2 \)
5. Volume: \( 0.4463495408 \times 0.6 \)
   • \(= 0.2678097245 \, \text{m}^3 \)

Convert to liters: \( 0.2678097245 \times 1000 = 267.810 \, \text{L} \)

12: Horizontal Cylinder with Dish Ends

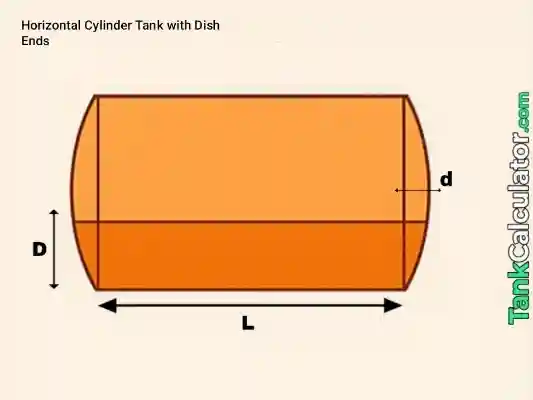
Formula:  \( V = \pi r^2 L_c + 2 \cdot V_{\text{cap}}, \quad V_{\text{cap}} = \pi d^2 \frac{(3R – d)}{3} \)

Example inputs: Diameter (\( D \)) = 0.6 m, Cylinder length (\( L_c \)) = 0.5 m, Dish depth (\( d \)) = 0.1 m, Radius (\( r = R = \frac{D}{2} \)) = 0.3 m

Calculation:

1. Cylinder volume: \( \pi r^2 L_c = \pi \times (0.3)^2 \times 0.5\)
   • \(= \pi \times 0.09 \times 0.5 \)
   • \(\approx 0.1413716694 \, \text{m}^3 \)
2. Cap volume (one cap): \( V_{\text{cap}} = \pi \times (0.1)^2 \times \frac{(3 \times 0.3 – 0.1)}{3}\)
   • \( = \pi \times 0.01 \times \frac{0.8}{3} \)
   • \(\approx 0.0083775804 \, \text{m}^3 \)
3. Two caps: \( 2 \times 0.0083775804\)
   • \( \approx 0.0167551608 \, \text{m}^3 \)

Total: \( 0.1413716694 + 0.0167551608 \)

\(\approx 0.1581268302 \, \text{m}^3 \)

Convert to liters: \( 0.1581268302 \times 1000 \approx 158.127 \, \text{liters}\)

13: Spherical Tank

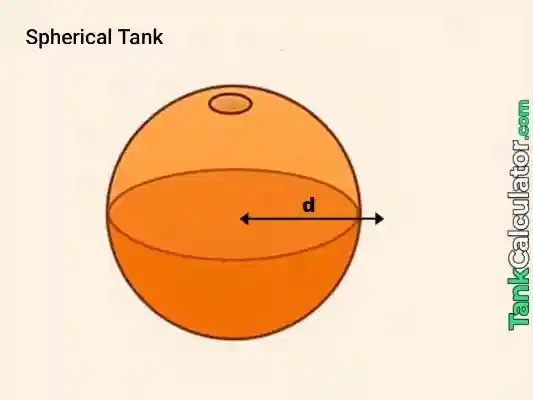
Formula: \( V = \frac{4}{3} \pi r^3 \) with \( r = D/2 \)

Example inputs:  \( D = 0.8 \, \text{m} \)

Calculation:

1. \( r = 0.4 \, \text{m} \)
2. \( r^3 = 0.064 \)
3. \( V = \frac{4}{3} \pi \times 0.064 \)
   • \(= 0.2680825731 \, \text{m}^3 \)

Convert to liters: \( 0.2680825731 \times 1000 = 268.083 \, \text{L} \)

14: Cylinder with Cone Bottom

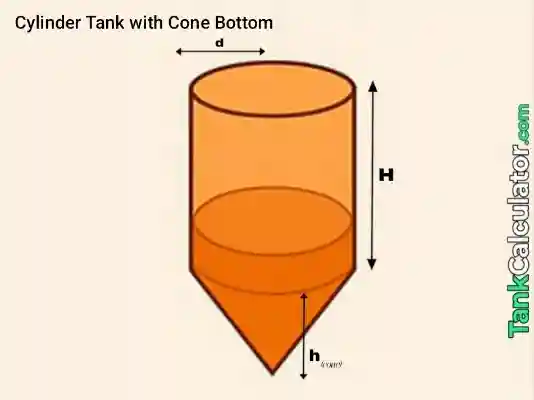
Formula: \( V = \pi r^2 H_{cyl} + \frac{1}{3} \pi r^2 H_{cone} \)

Example inputs: \( D = 0.6 \, \text{m}, H_{cyl} = 0.6 \, \text{m}, H_{cone} = 0.3 \, \text{m} \)

Calculation:

1. \( r = 0.3 \, \text{m}, r^2 = 0.09 \)
2. Cylinder: \( \pi r^2 H_{cyl} = \pi \times 0.09 \times 0.6\)
   • \( = 0.1696460033 \, \text{m}^3 \)
3. Cone: \( \frac{1}{3} \pi r^2 H_{cone} = \frac{1}{3} \pi \times 0.09 \times 0.3 \)
   • \(= 0.0282743339 \, \text{m}^3 \)

Total: \( 0.1696460033 + 0.0282743339 \)

\(= 0.1979203372 \, \text{m}^3 \)

Convert to liters: \( 0.1979203372 \times 1000 = 197.920 \, \text{L} \)

These aren’t exotic math tricks. They’re just standard geometry applied to practical problems.

Features and Benefits of a Water Tank Capacity Calculator

So why bother with a water tank capacity calculator instead of doing it by hand? Here is what stands out:

• Multiple shapes covered. From basic boxes to tricky capsule or dish end tanks, you don’t need to remember different formulas.

• Unit flexibility. Input dimensions in meters, centimeters, inches or feet. The tool automatically converts everything to cubic meters before calculating.

• Instant conversions. Once the volume is known, you get it in liters, US gallons, UK gallons and cubic feet. No more searching conversion tables.

• Printable and exportable results. You can print your results or download them as a CSV file, handy for engineers, plumbers or students working on reports.

• User friendly. It is designed for anyone whether you are a farmer checking tank size, a builder planning a water supply system or just curious about your rain barrel.

Which is the Best Water Tank Company in India?

If you’re setting up a new home or replacing an old tank, the question comes up quickly: which brand should I trust? After all, a water tank is not something that you change every year. You want it to be safe, sturdy, hassle free and durable.

In India, the best water tanks usually share a few qualities: they are made of food grade plastic (so the water does not pick up taste or smell), they have UV protection (so the sun doesn’t wear them out) and they often come with multiple layers to keep the water cool and clean in sunny days.

A few names keep coming up in conversations link: Sintex, Supreme, Vectus, Ashirvad and Plasto. They have been around for years and each has its own strengths. Let’s compare them side by side:

Brand	Why People Choose It	Typical Tank Sizes
Sintex	The “household name.” Tough, UV-stable, and widely available.	500L – 20,000L
Supreme	Reliable plastic quality and long lifespan. Great for big family homes.	500L – 10,000L
Vectus	Sleek designs plus durability. Good if you care about looks too.	500L – 5,000L
Ashirvad	Premium tanks with anti-microbial coating for cleaner water.	500L – 10,000L
Plasto	Budget-friendly option that’s easy to find locally.	500L – 5,000L

Frequently Asked Questions (FAQ)

---